A-double-flat 4th intervals
The Solution below shows the 4th note intervals above note Abb, and their inversions on the piano, treble clef and bass clef.
The Lesson steps then explain how to calculate each note interval name, number, spelling and quality. The final lesson step explains how to invert each interval.
For a quick summary of this topic, and to see the important interval table used to calculate the number of semitones in each interval, have a look at Note interval.
| Key | C | C# | Db | D | D# | Eb | E | E# | Fb | F | F# | Gb | G | G# | Ab | A | A# | Bb | B | B# | Cb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Interval no | 1st | 2nd | 3rd | [4th] | 5th | 6th | 7th | 8th |
Solution
1. A-double-flat dim4-perf4-aug4 intervals
4th intervals above note A-double-flat
| Short | Medium | Spelling / formula | Intervals 'above' statement | #Semitones |
|---|---|---|---|---|
| d4 | dim4 | b4 | The Abb to Dbbb interval is diminished 4th | 4 |
| P4 | perf4 | 4 | The Abb to Dbb interval is perfect 4th | 5 |
| A4 | aug4 | #4 | The Abb to Db interval is augmented 4th | 6 |
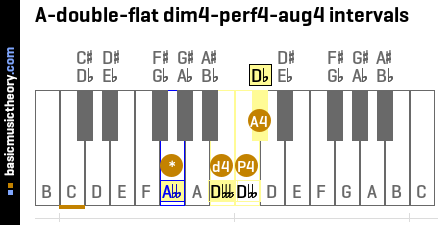
Middle C (midi note 60) is shown with an orange line under the 2nd note on the piano diagram.
These intervals are shown below on the treble clef followed by the bass clef.


Inverted intervals identifying note A-double-flat
This table inverts the above intervals, so that each link in the last column leads to note A-double-flat.
| Short | Medium | Long | Note name | Link to inverted interval |
|---|---|---|---|---|
| d4 | Abbdim4 | A-double-flat diminished 4th | Dbbb | <-(!?)-> B-aug-5th |
| P4 | Abbperf4 | A-double-flat perfect 4th | Dbb | Dbb-perf-5th |
| A4 | Abbaug4 | A-double-flat augmented 4th | Db | Db-dim-5th |
4th intervals below note A-double-flat
| Short | Medium | Intervals 'below' statement |
|---|---|---|
| d4 | dim4 | The diminished 4th interval below Dbbb is Abb |
| P4 | perf4 | The perfect 4th interval below Dbb is Abb |
| A4 | aug4 | The augmented 4th interval below Db is Abb |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
Lesson steps
1. Piano key note names
The white keys are named using the alphabetic letters A, B, C, D, E, F, and G, which is a pattern that repeats up the piano keyboard.
Every white or black key could have a flat(b) or sharp(#) accidental name, depending on how that note is used. In a later step, if sharp or flat notes are used, the exact accidental names will be chosen.
The audio files below play every note shown on the piano above, so middle C (marked with an orange line at the bottom) is the 2nd note heard.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
2. A-double-flat major note interval positions
The major scale uses the W-W-H-W-W-W-H note counting rule to identify the scale note positions.
To count up a Whole tone, count up by two physical piano keys, either white or black.
To count up a Half-tone (semitone), count up from the last note up by one physical piano key, either white or black.
The tonic note - Abb ,shown with an asterisk (*), is the starting point and is always the 1st note in the major scale.
The tonic is also the note from which intervals will be calculated in later steps - ie. all calculated intervals will have higher note pitches than the tonic.
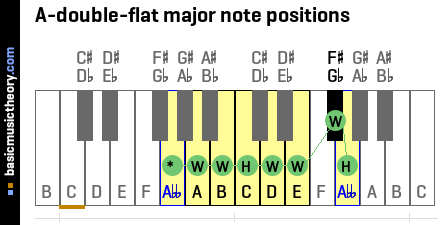
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Note | Abb | A | B | C | D | E | F# / Gb | Abb |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
3. A-double-flat major interval qualities
The table and piano diagram below show the 8 notes (7 scale major notes + octave note) in the Abb major scale together with the interval quality for each.
Perfect or major?
The interval quality for each note in this major scale is always perfect or major. So the 1st, 4th, 5th and 8th are always perfect, and the rest are always major. This rule is fixed all major scales in all keys, so you will never see a perfect 3rd or a major 4th interval.
The difference between the perfect and major intervals is that perfect interval notes sound more perfect / pleasing to the ear than major intervals - ie. are more consonant / less disonant, when played together (harmonic interval) with, or alongside(melodic interval) the tonic note.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Note | Abb | Bbb | Cb | Dbb | Ebb | Fb | Gb | Abb |
| #Semitones | 0 | 2 | 4 | 5 | 7 | 9 | 11 | 12 |
| Quality | perfect | major | major | perfect | perfect | major | major | perfect |
| Spelling / formula | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
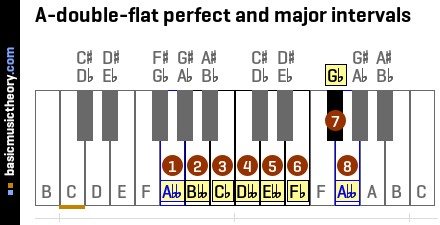
Interval spelling / formula
In music theory, note intervals can also be expressed using using a spelling or formula, which mean the same thing. You may have seen a chord expressed as 1 b3 5, for example.
The spelling of the interval qualities in the above table will always be shown without any sharp(#) or flat(b) symbols, since these extra symbols represent the difference of the note from the major scale. And since the above table shows the intervals of the major scale, no sharp / flat adjustments are needed.
Using just the notes we have in the major scale above, a chord spelling of 1 3 5 uses the 1st, 3rd and 5th notes as they are, ie. the Abb major chord. Or a 1 3 5 7 chord adds the extra 7th note, ie. the uses the 1st, 3rd and 5th notes as they are, ie. the Abb maj 7 chord.
This rest of this page will focus on the relationship between the tonic note - Abb, and the intervals surrounding the 4th major scale note - Dbb, whose interval quality is perfect. So we will definitely see extra sharp or flat spelling symbols there.
4. A-double-flat 4th interval pitches
Having established that the perfect 4th interval of the Abb major scale is note Dbb, this step will explore the other 4th intervals next this note.
A perfect interval usually has 2 other intervals grouped around it - one higher and one lower:
> One half-tone / semitone up from the perfect interval is the augmented interval.
> One half-tone / semitone down from the perfect interval is the diminished interval.
The interval number (4th) is added to the end, resulting in interval names going from the lowest note pitch to the highest:
| Short | Medium | Long | Spelling / formula | #Semitones |
|---|---|---|---|---|
| d4 | dim4 | diminished 4th | b4 | 4 |
| P4 | perf4 | perfect 4th | 4 | 5 |
| A4 | aug4 | augmented 4th | #4 | 6 |
Interval spelling / formula
Each interval has a spelling that represents its position relative to the perfect interval.
Flat signs (b) are used for intervals lower, and sharp (#) for intervals higher.
Interval short and medium names
Each interval name also has short and medium abbreviations, which are just different names for the same interval that you might see.
The short names are used in the piano diagram below to show the exact interval positions, with the orange number 0 representing the perfect interval, and the other orange numbers showing the number of half-tones / semitones up or down relative to that perfect interval.
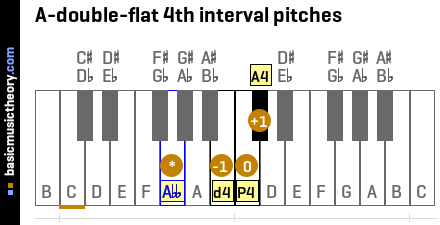
The exact note names, including sharps and flats, of each of these intervals will be covered in the next step.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
5. A-double-flat 4th intervals
To calculate the correct interval names, just like the previous step, the perfect 4th note is used as the starting point for working out interval information around it.
The perfect 4th note name is Dbb, and so all intervals around it must start with the note name D, ie. be a variation of that name, with either sharps or flats used describe the interval difference in half-tones / semitones from any given interval note to the perfect 4th.
Sharps or flats will be added or cancelled to force all interval names to start with D. Even if that involves using double and triple-sharps and flats.
| Short | Medium | Long | Spelling / formula | Note name | #Semitones |
|---|---|---|---|---|---|
| d4 | Abbdim4 | A-double-flat diminished 4th | b4 | Dbbb | 4 |
| P4 | Abbperf4 | A-double-flat perfect 4th | 4 | Dbb | 5 |
| A4 | Abbaug4 | A-double-flat augmented 4th | #4 | Db | 6 |
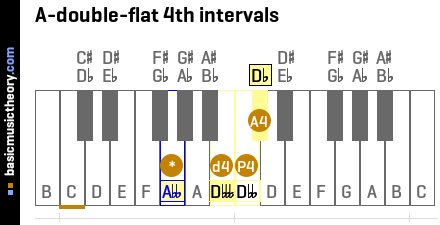
Middle C (midi note 60) is shown with an orange line under the 2nd note on the piano diagram.
These intervals are shown below on the treble clef followed by the bass clef.


But why is this done ? To get the missing piece of the puzzle, we need to return to the interval number - the 4th.
Not only does this number describe the note number of the perfect interval in the major scale, but it also describes the number of either lines or spaces on the staff between the tonic note and all intervals sharing that number - 4th, be they called diminished, minor, major, perfect or augmented.
On either the treble or bass clef above, count the number of lines and spaces - starting from 1 at the tonic note (the lowest note), and ending on a given interval, and the last line or space having the interval you want will be 4th line or space.
So this naming system forces all related 4th intervals to share the same treble / bass clef line or space, as ultimately they are all 4ths, but each interval having different interval quality names (major, minor, diminished etc).
However, this explanation does not hold for intervals that are measured starting from double sharps or flats, but is useful in other cases.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
6. A-double-flat 4th inverted intervals
Note interval inversion
An inverted interval is just an interval that is turned upside down.
For example, in the steps above, one of the intervals we measured was a perfect 4th above Abb, which is note Dbb.
In contrast, an inverted interval specifies the distance from Dbb to Abb - ie. note Abb is above note Dbb.
A set of fixed rules exist to help us calculate the new quality name and interval number:
Note interval quality inversion rules
> A major interval always inverts to a minor interval.
> A minor interval always inverts to a major interval.
> A perfect interval always inverts to a perfect interval - no change.
> A diminished interval always inverts to a augmented interval.
> An augmented interval always inverts to a diminished interval.
Note interval number inversion rules
Simply subtract the original interval number from 9, resulting in the inverted interval number.
A-double-flat 4th interval inversions
Taking the above rules into account, below is the table shown in the previous step, but with an extra column at the end for the link to the inverted interval quality in each case.
| Short | Medium | Long | Note name | Link to inverted interval |
|---|---|---|---|---|
| d4 | Abbdim4 | A-double-flat diminished 4th | Dbbb | <-(!?)-> B-aug-5th |
| P4 | Abbperf4 | A-double-flat perfect 4th | Dbb | Dbb-perf-5th |
| A4 | Abbaug4 | A-double-flat augmented 4th | Db | Db-dim-5th |
One or more of the inverted intervals in the last column are marked <-(!?)->, meaning that the note from which the inverted interval would be measured is not common, and so an enharmonic (simpler) note is given.
The note pitches, interval number and quality do not change.
Related Keys and Topics
| Key | C | C# | Db | D | D# | Eb | E | E# | Fb | F | F# | Gb | G | G# | Ab | A | A# | Bb | B | B# | Cb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Interval no | 1st | 2nd | 3rd | [4th] | 5th | 6th | 7th | 8th |
| Related links | A-double-flat 4th intervals, Abb major scale, Abb |
|---|---|
| Minor scales | Abb natural minor scale, Abb harmonic minor scale, Abb melodic minor scale |
| Circle of 5ths | Learn the circle of fifths |
| Triad chords | Abb diminished, Abb minor, Abb major, Abb augmented, Abb suspended 2nd, Abb suspended 4th |
| 6th chords | Abb minor 6th, Abb major 6th |
| 7th chords | Abb dim 7, Abb half-dim7, Abb min 7, Abb min-maj 7, Abb dom 7, Abb maj 7, Abb aug 7, Abb aug-maj 7, Abb maj 7 sus2, Abb dom 7 sus4, Abb maj 7 sus4 |
| Cadences | Abb major perfect authentic, Abb major imperfect authentic, Abb major plagal, Abb major half, Abb major deceptive |