Note interval
A note interval describes the relationship, and the number of half-tones / semitones / piano keys between two different notes.
Note intervals are commonly used in music theory to identify the individual note names of chords.
Note interval components
A note interval is made up of 3 components.
The first component is a note name eg, Eb, which is the note above which the interval is measured, ie. we want to measure an interval starting from note Eb
The second component is the interval number, which is a note number of the major scale whose tonic is the note name. ie. we want to measure from the starting note up to eg. the 3rd note of the major scale.
The third component is an interval quality, which might be a pitch adjustment, up or down, to the note at the interval number.
Note interval qualities
Note interval qualities are called diminished, minor, major, perfect and augmented. eg. we want to measure from the starting note up to eg. the 3rd note of the major scale, with a diminished quality.
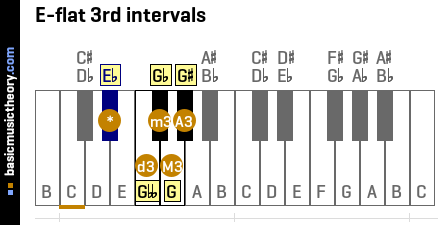
The piano diagram below shows all the note interval qualities of the Eb-3rd interval.
Note interval table
Below is a table showing all note intervals that can be measured starting from any note name on the piano.
| #Semitones | Short name | Quality | Interval no. | Spelling / formula |
|---|---|---|---|---|
| 0 | P1 | perfect | 1 | 1 |
| 0 | d2 | diminished | 2 | bb2 |
| 1 | m2 | minor | 2 | b2 |
| 1 | A1 | augmented | 1 | #1 |
| 2 | M2 | major | 2 | 2 |
| 2 | d3 | diminished | 3 | bb3 |
| 3 | m3 | minor | 3 | b3 |
| 3 | A2 | augmented | 2 | #2 |
| 4 | M3 | major | 3 | 3 |
| 4 | d4 | diminished | 4 | b4 |
| 5 | P4 | perfect | 4 | 4 |
| 5 | A3 | augmented | 3 | #3 |
| 6 | d5 | diminished | 5 | b5 |
| 6 | A4 | augmented | 4 | #4 |
| 7 | P5 | perfect | 5 | 5 |
| 7 | d6 | diminished | 6 | bb6 |
| 8 | m6 | minor | 6 | b6 |
| 8 | A5 | augmented | 5 | #5 |
| 9 | M6 | major | 6 | 6 |
| 9 | d7 | diminished | 7 | bb7 |
| 10 | m7 | minor | 7 | b7 |
| 10 | A6 | augmented | 6 | #6 |
| 11 | M7 | major | 7 | 7 |
| 11 | d8 | diminished | 8 | b8 |
| 12 | P8 | perfect | 8 | 8 |
| 12 | A7 | augmented | 7 | #7 |
Column ordering
Each semitone number(first column) is used twice, which means that it is never possible to calculate the name of an interval by counting only the number of half-tones / semitones. The interval number (last column) is needed too.
For example, the interval distance of 5 half-tones / semitones between two notes could be called a perfect 4th or an augmented 3rd.
Using our E-flat scale to demonstrate this, the Eb-perf-4th (A-flat) and Eb-aug-3rd (G-sharp) intervals have the same distance in half-tones / semitones.
This is not surprising, since A-flat and G-sharp are different names for the same note on a piano keyboard.
Major and perfect interval groupings
When it comes to identifying the name of a note for an interval, the name of the perfect or major interval is used as a starting point from which the other intervals grouped around it are named.
Remember the 1st, 4th, 5th and 8th notes of a major scale are always perfect, and the others - 2nd, 3rd, 6th and 7th are aways major.
So you will never see a perfect 3rd, or a major 5th interval.
Interval spelling / formula
In music theory, note intervals can also be expressed using using a spelling or formula, which mean the same thing. You may have seen a chord expressed as 1 b3 5, for example.
Each interval has a spelling that represents its position relative to the major or perfect interval of the same interval number. Flat signs (b) are used for intervals lower, and sharp (#) for intervals higher.
The final column shows all spellings, and as you can see it is even possible for an interval to be two notes lower (bb) than a major interval
Interval quality names differ by group
Be aware that the interval qualities around major qualities are different to those around perfect qualities.
Using the above example, a perfect interval eg. Eb-perf-4th has a diminished quality 1 half-tone / semitone down from it.
Compare this to, a major interval eg. Eb-aug-3rd, which has a diminished quality 2 half-tones / semitones down from it.
When starting out exploring intervals using the links above, always be aware to choose a perfect and a major interval to compare the the quality name differences between them.
However, to start off, suggest comparing the intervals around two different perfect intervals eg. Eb-perf-4th and Eb-perf-5th, while keeping the above table to hand as a reference.
Then compare the intervals around two different major intervals eg. Eb-maj-3rd and Eb-maj-6th.
Finally, compare a major and perfect interval eg. Eb-aug-3rd and Eb-perf-4th, to demonstrate that two different quality names can occupy the same piano key ie. from the table above, both P4 and A3 are 5 semitones from the base note - E-Flat.
How to invert an interval
An inverted interval is just an interval that is turned upside down.
For example, one of the intervals we identified about was an augmented 3rd above Eb, which is note G#.
In contrast, an inverted interval specifies the distance from G# to Eb - ie. note Eb is above note G#.
A set of fixed rules exist to help us calculate the new quality name and interval number:
Note interval quality inversion rules
> A major interval always inverts to a minor interval.
> A minor interval always inverts to a major interval.
> A perfect interval always inverts to a perfect interval - no change.
> A diminished interval always inverts to a augmented interval.
> An augmented interval always inverts to a diminished interval.
So in our example - an augmented 3rd above Eb, the original interval is augmented, which inverts to diminished.
Note interval number inversion rules
Simply subtract the original interval number from 9, resulting in the inverted interval number.
For our example - an augmented 3rd above E-flat, we subtract 3 from 9, leaving the inverted interval number 6 - ie. a 6th above G#.
Putting it all together, the original interval - Eb-aug-3rd inverts to G#-dim-6th, which means that G#-dim-6th will take you to note Eb, the note above which we calculated our original interval.