A-flat 1st intervals
The Solution below shows the 1st note intervals above note Ab, and their inversions on the piano, treble clef and bass clef.
The Lesson steps then explain how to calculate each note interval name, number, spelling and quality. The final lesson step explains how to invert each interval.
For a quick summary of this topic, and to see the important interval table used to calculate the number of semitones in each interval, have a look at Note interval.
| Key | C | C# | Db | D | D# | Eb | E | E# | Fb | F | F# | Gb | G | G# | [Ab] | A | A# | Bb | B | B# | Cb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Interval no | [1st] | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th |
Solution
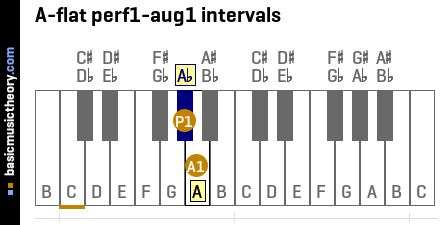
1. A-flat perf1-aug1 intervals
1st intervals above note A-flat
| Short | Medium | Spelling / formula | Intervals 'above' statement | #Semitones |
|---|---|---|---|---|
| P1 | perf1 | 1 | The Ab to Ab interval is perfect Unison | 0 |
| A1 | aug1 | #1 | The Ab to A interval is augmented Unison | 1 |
Middle C (midi note 60) is shown with an orange line under the 2nd note on the piano diagram.
These intervals are shown below on the treble clef followed by the bass clef.


Inverted intervals identifying note A-flat
This table inverts the above intervals, so that each link in the last column leads to note A-flat.
| Short | Medium | Long | Note name | Link to inverted interval |
|---|---|---|---|---|
| P1 | Abperf1 | A-flat perfect Unison | Ab | Ab-perf-8th |
| A1 | Abaug1 | A-flat augmented Unison | A | A-dim-8th |
1st intervals below note A-flat
| Short | Medium | Intervals 'below' statement |
|---|---|---|
| P1 | perf1 | The perfect Unison interval below Ab is Ab |
| A1 | aug1 | The augmented Unison interval below A is Ab |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
Lesson steps
1. Piano key note names
The white keys are named using the alphabetic letters A, B, C, D, E, F, and G, which is a pattern that repeats up the piano keyboard.
Every white or black key could have a flat(b) or sharp(#) accidental name, depending on how that note is used. In a later step, if sharp or flat notes are used, the exact accidental names will be chosen.
The audio files below play every note shown on the piano above, so middle C (marked with an orange line at the bottom) is the 2nd note heard.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
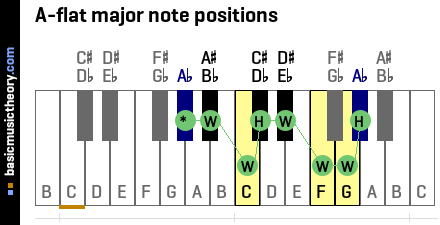
2. A-flat major note interval positions
The major scale uses the W-W-H-W-W-W-H note counting rule to identify the scale note positions.
To count up a Whole tone, count up by two physical piano keys, either white or black.
To count up a Half-tone (semitone), count up from the last note up by one physical piano key, either white or black.
The tonic note - Ab ,shown with an asterisk (*), is the starting point and is always the 1st note in the major scale.
The tonic is also the note from which intervals will be calculated in later steps - ie. all calculated intervals will have higher note pitches than the tonic.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Note | Ab | A# / Bb | C | C# / Db | D# / Eb | F | G | Ab |
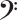 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
3. A-flat major interval qualities
The table and piano diagram below show the 8 notes (7 scale major notes + octave note) in the Ab major scale together with the interval quality for each.
Perfect or major?
The interval quality for each note in this major scale is always perfect or major. So the 1st, 4th, 5th and 8th are always perfect, and the rest are always major. This rule is fixed all major scales in all keys, so you will never see a perfect 3rd or a major 4th interval.
The difference between the perfect and major intervals is that perfect interval notes sound more perfect / pleasing to the ear than major intervals - ie. are more consonant / less disonant, when played together (harmonic interval) with, or alongside(melodic interval) the tonic note.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Note | Ab | Bb | C | Db | Eb | F | G | Ab |
| #Semitones | 0 | 2 | 4 | 5 | 7 | 9 | 11 | 12 |
| Quality | perfect | major | major | perfect | perfect | major | major | perfect |
| Spelling / formula | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Interval spelling / formula
In music theory, note intervals can also be expressed using using a spelling or formula, which mean the same thing. You may have seen a chord expressed as 1 b3 5, for example.
The spelling of the interval qualities in the above table will always be shown without any sharp(#) or flat(b) symbols, since these extra symbols represent the difference of the note from the major scale. And since the above table shows the intervals of the major scale, no sharp / flat adjustments are needed.
Using just the notes we have in the major scale above, a chord spelling of 1 3 5 uses the 1st, 3rd and 5th notes as they are, ie. the Ab major chord. Or a 1 3 5 7 chord adds the extra 7th note, ie. the uses the 1st, 3rd and 5th notes as they are, ie. the Ab maj 7 chord.
This rest of this page will focus on the relationship between the tonic note - Ab, and the intervals surrounding the 1st major scale note - Ab, whose interval quality is perfect. So we will definitely see extra sharp or flat spelling symbols there.
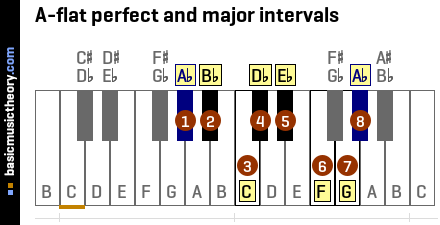
4. A-flat 1st interval pitches
Having established that the perfect 1st interval of the Ab major scale is note Ab, this step will explore the other 1st intervals next this note.
A perfect interval usually has 2 other intervals grouped around it - one higher and one lower:
> One half-tone / semitone up from the perfect interval is the augmented interval.
> One half-tone / semitone down from the perfect interval is the diminished interval.
However, for this perfect interval (1st), the diminished interval does not exist ie. does not make any sense in music theory.
The 1st interval also has a unique name - rather than calling it a 1st, it is usually referred to as Unison, as shown in the table below. The notes go from the lowest note pitch to the highest:
| Short | Medium | Long | Spelling / formula | #Semitones |
|---|---|---|---|---|
| P1 | perf1 | perfect Unison | 1 | 0 |
| A1 | aug1 | augmented Unison | #1 | 1 |
Interval spelling / formula
Each interval has a spelling that represents its position relative to the perfect interval.
Flat signs (b) are used for intervals lower, and sharp (#) for intervals higher.
Interval short and medium names
Each interval name also has short and medium abbreviations, which are just different names for the same interval that you might see.
The short names are used in the piano diagram below to show the exact interval positions, with the orange number 0 representing the perfect interval, and the other orange numbers showing the number of half-tones / semitones up or down relative to that perfect interval.
The exact note names, including sharps and flats, of each of these intervals will be covered in the next step.
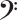 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
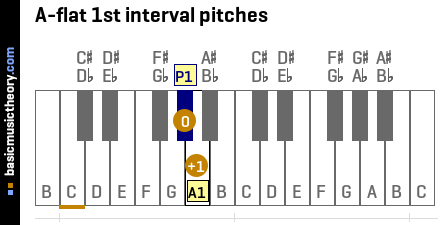
5. A-flat 1st intervals
To calculate the correct interval names, just like the previous step, the perfect 1st note is used as the starting point for working out interval information around it.
The perfect 1st note name is Ab, and so all intervals around it must start with the note name A, ie. be a variation of that name, with either sharps or flats used describe the interval difference in half-tones / semitones from any given interval note to the perfect 1st.
Sharps or flats will be added or cancelled to force all interval names to start with A. Even if that involves using double and triple-sharps and flats.
| Short | Medium | Long | Spelling / formula | Note name | #Semitones |
|---|---|---|---|---|---|
| P1 | Abperf1 | A-flat perfect Unison | 1 | Ab | 0 |
| A1 | Abaug1 | A-flat augmented Unison | #1 | A | 1 |
Middle C (midi note 60) is shown with an orange line under the 2nd note on the piano diagram.
These intervals are shown below on the treble clef followed by the bass clef.


But why is this done ? To get the missing piece of the puzzle, we need to return to the interval number - the 1st.
Not only does this number describe the note number of the perfect interval in the major scale, but it also describes the number of either lines or spaces on the staff between the tonic note and all intervals sharing that number - 1st, be they called diminished, minor, major, perfect or augmented.
On either the treble or bass clef above, count the number of lines and spaces - starting from 1 at the tonic note (the lowest note), and ending on a given interval, and the last line or space having the interval you want will be 1st line or space.
So this naming system forces all related 1st intervals to share the same treble / bass clef line or space, as ultimately they are all 1sts, but each interval having different interval quality names (major, minor, diminished etc).
However, this explanation does not hold for intervals that are measured starting from double sharps or flats, but is useful in other cases.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
6. A-flat 1st inverted intervals
Note interval inversion
An inverted interval is just an interval that is turned upside down.
For example, in the steps above, one of the intervals we measured was a perfect 1st above Ab, which is note Ab.
In contrast, an inverted interval specifies the distance from Ab to Ab - ie. note Ab is above note Ab.
A set of fixed rules exist to help us calculate the new quality name and interval number:
Note interval quality inversion rules
> A major interval always inverts to a minor interval.
> A minor interval always inverts to a major interval.
> A perfect interval always inverts to a perfect interval - no change.
> A diminished interval always inverts to a augmented interval.
> An augmented interval always inverts to a diminished interval.
Note interval number inversion rules
Simply subtract the original interval number from 9, resulting in the inverted interval number.
A-flat 1st interval inversions
Taking the above rules into account, below is the table shown in the previous step, but with an extra column at the end for the link to the inverted interval quality in each case.
| Short | Medium | Long | Note name | Link to inverted interval |
|---|---|---|---|---|
| P1 | Abperf1 | A-flat perfect Unison | Ab | Ab-perf-8th |
| A1 | Abaug1 | A-flat augmented Unison | A | A-dim-8th |
Related Keys and Topics
| Key | C | C# | Db | D | D# | Eb | E | E# | Fb | F | F# | Gb | G | G# | [Ab] | A | A# | Bb | B | B# | Cb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Interval no | [1st] | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th |