A-sharp natural minor scale
The Solution below shows the A# minor scale notes, intervals and scale degrees on the piano, treble clef and bass clef.
The Lesson steps then explain how to identify the A-sharp minor scale note interval positions, choose the note names, and scale degree names.
For a quick summary of this topic, have a look at Natural minor scale.
| Key | C | C# | Db | D | D# | Eb | E | E# | Fb | F | F# | Gb | G | G# | Ab | A | [A#] | Bb | B | B# | Cb | All On 1 page |
|---|
Solution - 2 parts
1. A-sharp natural minor scale
The A-sharp natural minor scale has 7 sharps.
This minor scale key is on the Circle of 5ths - A# minor on circle of 5ths, which means that it is a commonly used minor scale key.
This scale sounds the same as the Bb natural minor scale, which is also a commonly used scale. The same notes are played in the same order in each scale - they sound identical. Only the names of the individual notes are different.
| Note no. | Note interval | Note name |
|---|---|---|
| 1 | tonic | The 1st note of the A-sharp natural minor scale is A# |
| 2 | A#-maj-2nd | The 2nd note of the A-sharp natural minor scale is B# |
| 3 | A#-min-3rd | The 3rd note of the A-sharp natural minor scale is C# |
| 4 | A#-perf-4th | The 4th note of the A-sharp natural minor scale is D# |
| 5 | A#-perf-5th | The 5th note of the A-sharp natural minor scale is E# |
| 6 | A#-min-6th | The 6th note of the A-sharp natural minor scale is F# |
| 7 | A#-min-7th | The 7th note of the A-sharp natural minor scale is G# |
| 8 | A#-perf-8th | The 8th note of the A-sharp natural minor scale is A# |
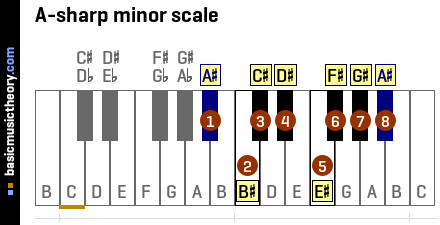
Middle C (midi note 60) is shown with an orange line under the 2nd note on the piano diagram.
These note names are shown below on the treble clef followed by the bass clef.


The stave diagrams above show the scale notes without a key signature, with the sharp / flat adjustments inserted before each note on the staff.
For the key signature of this scale, showing these symbols grouped correctly next to the bass or treble clef symbol at the beginning, have a look at the A# natural minor key signature.
| Note no. | Degree name |
|---|---|
| 1 | A# is the tonic of the A-sharp natural minor scale |
| 2 | B# is the supertonic of the A-sharp natural minor scale |
| 3 | C# is the mediant of the A-sharp natural minor scale |
| 4 | D# is the subdominant of the A-sharp natural minor scale |
| 5 | E# is the dominant of the A-sharp natural minor scale |
| 6 | F# is the submediant of the A-sharp natural minor scale |
| 7 | G# is the subtonic of the A-sharp natural minor scale |
| 8 | A# is the octave of the A-sharp natural minor scale |
The difference between the A-sharp natural minor scale and the A# major scale is that the 3rd, 6th and 7th note positions of the major scale are lowered by one half-tone / semitone.
So whereas the A# major scale has notes C##, F##, G## for the 3rd, 6th and 7th notes, these notes are lowered to arrive at notes C#, F#, G# for this natural minor scale.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
2. A-sharp natural minor scale descending
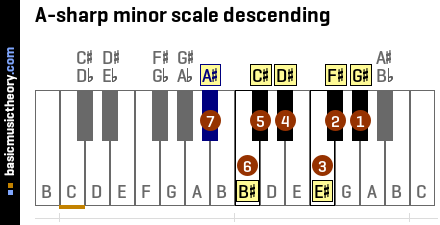


| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | G# | F# | E# | D# | C# | B# | A# |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
Lesson steps
1. Piano key note names
The white keys are named using the alphabetic letters A, B, C, D, E, F, and G, which is a pattern that repeats up the piano keyboard.
Every white or black key could have a flat(b) or sharp(#) accidental name, depending on how that note is used. In a later step, if sharp or flat notes are used, the exact accidental names will be chosen.
The audio files below play every note shown on the piano above, so middle C (marked with an orange line at the bottom) is the 2nd note heard.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
2. A-sharp tonic note and one octave of notes
The numbered notes are those that might be used when building this note scale.
But since this is a scale in the key of A#, it is certain that notes 1 and 13 will be used in the scale.
Note 1 is the tonic note - the starting note - A#, and note 13 is the same note name but one octave higher.
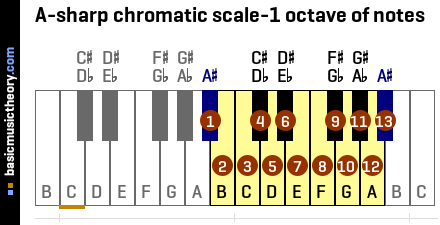
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Note | A# | B | C | C# / Db | D | D# / Eb | E | F | F# / Gb | G | G# / Ab | A | A# |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
3. A-sharp natural minor scale note interval positions
The natural minor scale uses the W-H-W-W-H-W-W note counting rule to identify the scale note positions.
To count up a Whole tone, count up by two physical piano keys, either white or black.
To count up a Half-tone (semitone), count up from the last note up by one physical piano key, either white or black.
The tonic note (shown as *) is the starting point and is always the 1st note in the natural minor scale.
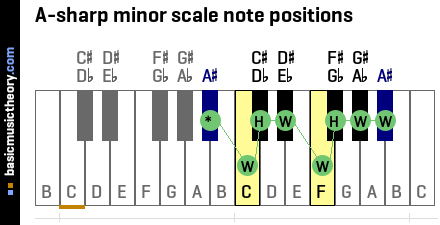
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Note | A# | C | C# / Db | D# / Eb | F | F# / Gb | G# / Ab | A# |
What is the difference between the A-sharp natural minor scale and the A# major scale ?
The 3rd, 6th and 7th note positions (or scale degrees) of the major scale are lowered by one half-tone / semitone to arrive at the minor scale note positions shown above.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
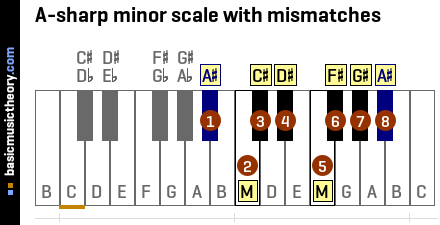
4. A-sharp natural minor scale notes
The 7 unique notes in a scale need to be named such that each letter from A to G is used once only, so each note name is either a natural white name(A.. G) , a sharp(eg. F#) or a flat(eg. Gb).
This is needed to ensure that when it comes to writing the scale notes on a musical staff (eg. a bass or treble clef), there is no possibility of having 2 G-type notes, for example, with one of the notes needing an accidental next to it on the staff (a sharp, flat or natural symbol).
To apply this rule, firstly list the white key names starting from the tonic, which are shown the White column below.
Then list the 7 notes in the scale so far, shown in the next column.
For each of the 7 notes, look across and try to find the White note name in the Scale note name.
If the natural white note can be found in the scale note, the scale note is written in the Match? column.
The 8th note - the octave note, will have the same name as the first note, the tonic note.
| No. | White | Scale note | Match? |
|---|---|---|---|
| 1 | A | A# | A# |
| 2 | B | C | m |
| 3 | C | C# / Db | C# |
| 4 | D | D# / Eb | D# |
| 5 | E | F | m |
| 6 | F | F# / Gb | F# |
| 7 | G | G# / Ab | G# |
| 8 | A | A# | A# |
For this scale, there are 2 mismatches (Shown as m in the Match? column), whose note names will need to be adjusted in the next step.
5. Make the A-sharp note name adjustments
The adjustment explanation below needs to be applied to every mismatch m in the above table. The first mismatch is used as an example.
The match fails when trying to find a B -type of scale note, because either this type of note does not exist in this scale, or it exists but is in the wrong position number / table row for this match.
But music theory rules allow the name of any note to be sharpened or flattened, even white note names, so since a B-type of note name is needed, the real scale note C will be renamed to B#.
Of course, even though the note is named B#, when it comes to playing the note on an instrument, the real note C is really played.
The adjustments done in this step do not change the pitch / sound of the note, only the name of the note.
After doing the adjustments to all mistmatches, all letters A..G will have been used for this minor scale, and no rules have been broken.
Note that sometimes it is necessary to adjust the note name two half-tones / semitones forward or back, which will result in an adjusted name containing a double-sharp or double-flat.
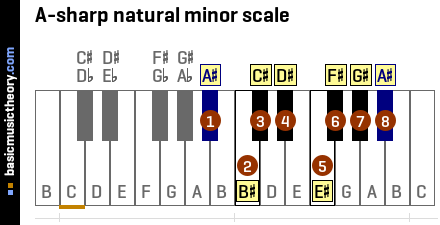
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Note | A# | B# | C# | D# | E# | F# | G# | A# |
6. A-sharp natural minor scale descending
For natural minor scales, the notes names when descending are just the reverse of the ascending names.
So assuming octave note 8 has been played in the step above, the notes now descend back to the tonic.

| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | G# | F# | E# | D# | C# | B# | A# |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
7. A-sharp natural minor scale degrees
Scale degree names 1,2,3,4,5,6, and 8 below are always the same for all major and minor scales (ie. 1st note is always tonic, 2nd is supertonic etc.) , but obviously the note names will be different for each scale / key combination.
In the natural minor scale, the 7th note is called the subtonic, and it has a whole tone (two half-tones / semitones, two notes on the piano keyboard) between the 7th and 8th notes in the scale.
In contrast, the A# major scale has only one half-tone / semitone separating the 7th and 8th notes, and in this case the seventh note is called the leading note or leading tone, as the 7th note feels like it wants to resolve and finish at the octave note, when all major scale notes are played in sequence.
Both the A# harmonic minor scale and A# melodic minor scale scales share the same property - having a leading tone, with the major scale.
| Note no. | Degree name |
|---|---|
| 1 | A# is the tonic of the A-sharp natural minor scale |
| 2 | B# is the supertonic of the A-sharp natural minor scale |
| 3 | C# is the mediant of the A-sharp natural minor scale |
| 4 | D# is the subdominant of the A-sharp natural minor scale |
| 5 | E# is the dominant of the A-sharp natural minor scale |
| 6 | F# is the submediant of the A-sharp natural minor scale |
| 7 | G# is the subtonic of the A-sharp natural minor scale |
| 8 | A# is the octave of the A-sharp natural minor scale |
Related Keys and Topics
| Key | C | C# | Db | D | D# | Eb | E | E# | Fb | F | F# | Gb | G | G# | Ab | A | [A#] | Bb | B | B# | Cb | All On 1 page |
|---|