A-sharp minor chords
The Solution below shows the A-sharp minor scale triad chords (i, iio, III, iv, v, VI, VII) on a piano, with mp3 and midi audio.
The Lesson steps then explain the triad chord construction from this scale, and how to name the quality of each chord based on note intervals.
For a quick summary of this topic, and to see the chord quality chart for this scale, have a look at Scale chord.
| Key | C | C# | Db | D | D# | Eb | E | E# | Fb | F | F# | Gb | G | G# | Ab | A | [A#] | Bb | B | B# | Cb |
|---|
Solution - 7 parts
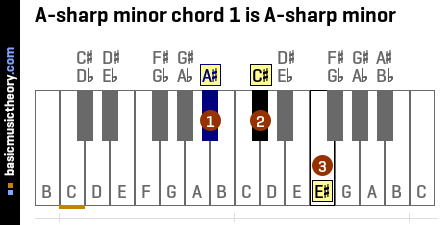
1. A-sharp minor chord i
Chord identification
The A-sharp minor chord i is the A# minor chord, and contains the notes A#, C#, and E#.
This tonic chord's root / starting note is the 1st note (or scale degree) of the A# natural minor scale.
The roman numeral for number 1 is 'i' and is used to indicate this is the 1st triad chord in the scale. It is in lower case to denote that the chord is a minor chord.
| Chord position | Link | a/b/c notation | Figured bass notation |
|---|---|---|---|
| Root position | A# minor chord in root position | ia | |
| 1st inversion | A# minor chord in 1st inversion | ib | i6 |
| 2nd inversion | A# minor chord in 2nd inversion | ic | i64 |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
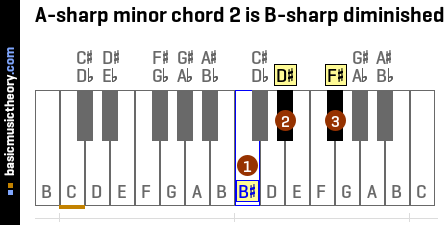
2. A-sharp minor chord iio
Chord identification
The A-sharp minor chord iio is the B# diminished chord, and contains the notes B#, D#, and F#.
This supertonic chord's root / starting note is the 2nd note (or scale degree) of the A# natural minor scale.
The roman numeral for number 2 is 'ii' and is used to indicate this is the 2nd triad chord in the scale. Just like a minor chord, the diminished chord is constructed using a minor third interval, so the roman numeral is shown in lower case.
The diminished symbol 'o' is placed after the roman numerals to indicate this is a diminished chord.
| Chord position | Link | a/b/c notation | Figured bass notation |
|---|---|---|---|
| Root position | B# diminished chord in root position | iioa | |
| 1st inversion | B# diminished chord in 1st inversion | iiob | iio6 |
| 2nd inversion | B# diminished chord in 2nd inversion | iioc | iio64 |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
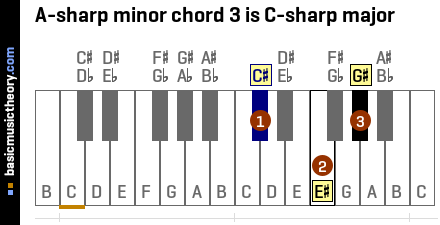
3. A-sharp minor chord III
Chord identification
The A-sharp minor chord III is the C# major chord, and contains the notes C#, E#, and G#.
This mediant chord's root / starting note is the 3rd note (or scale degree) of the A# natural minor scale.
The roman numeral for number 3 is 'III' and is used to indicate this is the 3rd triad chord in the scale. It is in upper case to denote that the chord is a major chord.
| Chord position | Link | a/b/c notation | Figured bass notation |
|---|---|---|---|
| Root position | C# major chord in root position | IIIa | |
| 1st inversion | C# major chord in 1st inversion | IIIb | III6 |
| 2nd inversion | C# major chord in 2nd inversion | IIIc | III64 |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
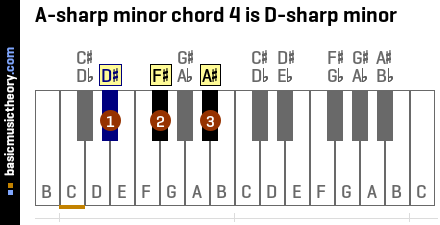
4. A-sharp minor chord iv
Chord identification
The A-sharp minor chord iv is the D# minor chord, and contains the notes D#, F#, and A#.
This subdominant chord's root / starting note is the 4th note (or scale degree) of the A# natural minor scale.
The roman numeral for number 4 is 'iv' and is used to indicate this is the 4th triad chord in the scale. It is in lower case to denote that the chord is a minor chord.
| Chord position | Link | a/b/c notation | Figured bass notation |
|---|---|---|---|
| Root position | D# minor chord in root position | iva | |
| 1st inversion | D# minor chord in 1st inversion | ivb | iv6 |
| 2nd inversion | D# minor chord in 2nd inversion | ivc | iv64 |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
5. A-sharp minor chord v
Chord identification
The A-sharp minor chord v is the E# minor chord, and contains the notes E#, G#, and B#.
This dominant chord's root / starting note is the 5th note (or scale degree) of the A# natural minor scale.
The roman numeral for number 5 is 'v' and is used to indicate this is the 5th triad chord in the scale. It is in lower case to denote that the chord is a minor chord.
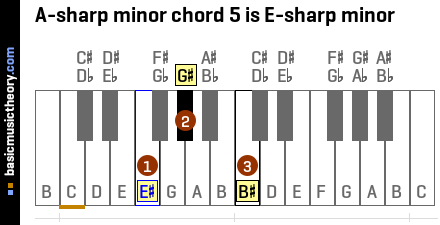
| Chord position | Link | a/b/c notation | Figured bass notation |
|---|---|---|---|
| Root position | E# minor chord in root position | va | |
| 1st inversion | E# minor chord in 1st inversion | vb | v6 |
| 2nd inversion | E# minor chord in 2nd inversion | vc | v64 |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
6. A-sharp minor chord VI
Chord identification
The A-sharp minor chord VI is the F# major chord, and contains the notes F#, A#, and C#.
This submediant chord's root / starting note is the 6th note (or scale degree) of the A# natural minor scale.
The roman numeral for number 6 is 'VI' and is used to indicate this is the 6th triad chord in the scale. It is in upper case to denote that the chord is a major chord.
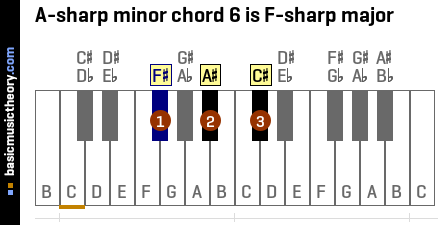
| Chord position | Link | a/b/c notation | Figured bass notation |
|---|---|---|---|
| Root position | F# major chord in root position | VIa | |
| 1st inversion | F# major chord in 1st inversion | VIb | VI6 |
| 2nd inversion | F# major chord in 2nd inversion | VIc | VI64 |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
7. A-sharp minor chord VII
Chord identification
The A-sharp minor chord VII is the G# major chord, and contains the notes G#, B#, and D#.
This subtonic chord's root / starting note is the 7th note (or scale degree) of the A# natural minor scale.
The roman numeral for number 7 is 'VII' and is used to indicate this is the 7th triad chord in the scale. It is in upper case to denote that the chord is a major chord.
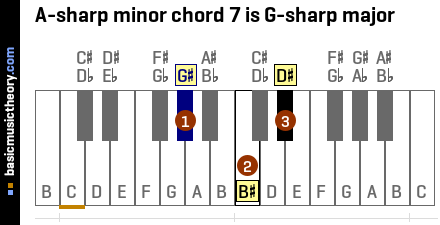
| Chord position | Link | a/b/c notation | Figured bass notation |
|---|---|---|---|
| Root position | G# major chord in root position | VIIa | |
| 1st inversion | G# major chord in 1st inversion | VIIb | VII6 |
| 2nd inversion | G# major chord in 2nd inversion | VIIc | VII64 |
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
Lesson steps
1. Piano key note names
The white keys are named using the alphabetic letters A, B, C, D, E, F, and G, which is a pattern that repeats up the piano keyboard.
Every white or black key could have a flat(b) or sharp(#) accidental name, depending on how that note is used. In a later step, if sharp or flat notes are used, the exact accidental names will be chosen.
The audio files below play every note shown on the piano above, so middle C (marked with an orange line at the bottom) is the 2nd note heard.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
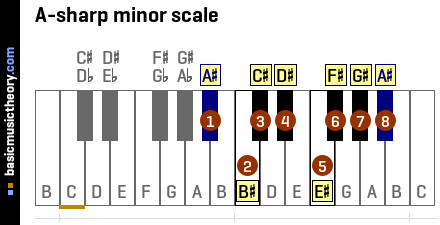
2. A-sharp minor scale notes
The piano keyboard below contains the notes of the A# natural minor scale.
Starting from the 1st scale note, each lesson step below will take each note in turn and construct a triad chord using that note as the root / starting note of that chord.
The triad chord will be built using only the notes of the scale we are interested in.
Identifying the 3 notes in the chord
Triad chords are built using the 1st, 3rdand 5th notes of the scale, so the first triad below will constructed a chord using notes A#, C# and E#.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Note | A# | B# | C# | D# | E# | F# | G# | A# |
The second triad below will repeat this, but this time starting on the 2nd note, so its notes will be B#, D# and F# - ie. the 1st, 3rd and 5th positions relative to that 2nd root note.
This pattern is repeated for all 7 notes in the scale, resulting in 7 triad chords.
Identifying the chord quality
Although the above method identifies each triads notes from the scale used - it does not identify the complete chord name including its quality.
Should each triad that we build be called major, minor, augmented, or diminished ? Every triad chord must have one of these quality names.
To decide the name the chord quality, each step below will use note intervals to calculate how many half-tones / semitones / piano keys between the root and the 3rd (and 5th).
Taken together, the combination of the 3rd and 5th note intervals will define the complete triad quality name.
The steps below will show how this works for each triad in turn, but in practice it might just be easier to memorize the triad quality table in the Scale chord summary for each scale type.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
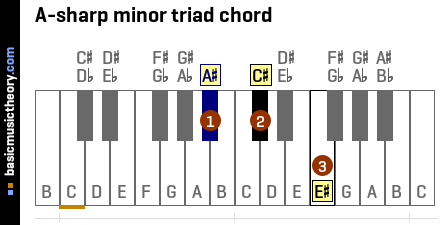
3. 1st triad chord in A-sharp minor scale
Identifying the 3 notes in the chord
The table below shows the A# natural minor scale, ordered to show the 1st note as the first column in the table.
To identify the triad chord note names, use the 1st, 3rd, and 5th columns / scale degrees, which are notes A#, C#, and E#.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | A# | B# | C# | D# | E# | F# | G# |
Identifying the chord quality
To identify the triad chord quality that has these notes, begin by counting the number of half-tones / semitones between the root and each of the notes.
For the 3rd Interval (note 2 on the diagram) the distance between A# and C# is 3 half-tones.
Now look at the complete Note interval table, and identify the note interval that has a distance of 3 half-tones (first column), and with an interval no. of 3 (last column).
The note interval name for the 3rd note / scale degree is therefore minor, also called m3 for short. More details of this interval are at A#-min-3rd.
Repeating this for the 5th note / scale degree, the distance between A# and E# is 7 half-tones, and the note interval name is perfect (P5). More details of this interval are at A#-perf-5th.
Finally, we have the name of the two note intervals of this triad, and can now lookup the name of the triad chord quality having these intervals.
Looking at the Triad chord table, the name of the triad chord quality having minor(m3) and perfect(P5) note intervals is minor.
And so the complete triad chord name prefixes the root note, A#, onto this quality, giving us the A# minor chord.
Scale chord names using a,b and c notation
The chord symbol i could be followed by the letter a to indicate that it is A# minor chord in root position (ie not inverted) - A-sharp minor scale chord ia.
Instead, i could be followed by the letter b to indicate that it is A# minor chord in 1st inversion - A-sharp minor scale chord ib.
Finally, letter c could be used to indicate that it is A# minor chord in 2nd inversion - A-sharp minor scale chord ic.
Scale chord names using figured bass notation
In place of the b or c symbols above, figured bass symbols could be used to indicate inversions after the chord number symbols i:
So in this key, i6 refers to the A# minor chord in 1st inversion, and i64 refers to the A# minor chord in 2nd inversion.
The next scale chord
The next step will need to calculate the triad chord whose root / starting note is next scale note.
To do this, the first column we used in this step, A#, will be moved to the final column of the table.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
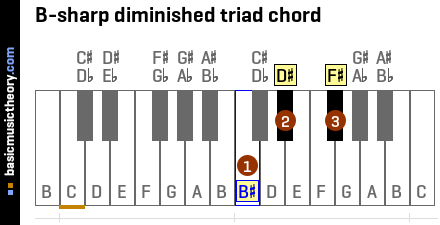
4. 2nd triad chord in A-sharp minor scale
Identifying the 3 notes in the chord
The table below shows the A# natural minor scale, ordered to show the 2nd note as the first column in the table.
To identify the triad chord note names, use the 1st, 3rd, and 5th columns / scale degrees, which are notes B#, D#, and F#.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | B# | C# | D# | E# | F# | G# | A# |
Identifying the chord quality
To identify the triad chord quality that has these notes, begin by counting the number of half-tones / semitones between the root and each of the notes.
For the 3rd Interval (note 2 on the diagram) the distance between B# and D# is 3 half-tones.
Now look at the complete Note interval table, and identify the note interval that has a distance of 3 half-tones (first column), and with an interval no. of 3 (last column).
The note interval name for the 3rd note / scale degree is therefore minor, also called m3 for short. More details of this interval are at B#-min-3rd.
Repeating this for the 5th note / scale degree, the distance between B# and F# is 6 half-tones, and the note interval name is diminished (d5). More details of this interval are at B#-dim-5th.
Finally, we have the name of the two note intervals of this triad, and can now lookup the name of the triad chord quality having these intervals.
Looking at the Triad chord table, the name of the triad chord quality having minor(m3) and diminished(d5) note intervals is diminished.
And so the complete triad chord name prefixes the root note, B#, onto this quality, giving us the B# diminished chord.
Scale chord names using a,b and c notation
The chord symbol iio could be followed by the letter a to indicate that it is B# diminished chord in root position (ie not inverted) - A-sharp minor scale chord iioa.
Instead, iio could be followed by the letter b to indicate that it is B# diminished chord in 1st inversion - A-sharp minor scale chord iiob.
Finally, letter c could be used to indicate that it is B# diminished chord in 2nd inversion - A-sharp minor scale chord iioc.
Scale chord names using figured bass notation
In place of the b or c symbols above, figured bass symbols could be used to indicate inversions after the chord number symbols iio:
So in this key, iio6 refers to the B# diminished chord in 1st inversion, and iio64 refers to the B# diminished chord in 2nd inversion.
The next scale chord
The next step will need to calculate the triad chord whose root / starting note is next scale note.
To do this, the first column we used in this step, B#, will be moved to the final column of the table.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
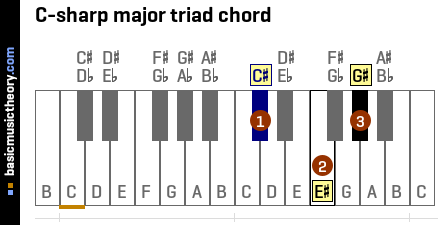
5. 3rd triad chord in A-sharp minor scale
Identifying the 3 notes in the chord
The table below shows the A# natural minor scale, ordered to show the 3rd note as the first column in the table.
To identify the triad chord note names, use the 1st, 3rd, and 5th columns / scale degrees, which are notes C#, E#, and G#.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | C# | D# | E# | F# | G# | A# | B# |
Identifying the chord quality
To identify the triad chord quality that has these notes, begin by counting the number of half-tones / semitones between the root and each of the notes.
For the 3rd Interval (note 2 on the diagram) the distance between C# and E# is 4 half-tones.
Now look at the complete Note interval table, and identify the note interval that has a distance of 3 half-tones (first column), and with an interval no. of 3 (last column).
The note interval name for the 3rd note / scale degree is therefore major, also called M3 for short. More details of this interval are at C#-maj-3rd.
Repeating this for the 5th note / scale degree, the distance between C# and G# is 7 half-tones, and the note interval name is perfect (P5). More details of this interval are at C#-perf-5th.
Finally, we have the name of the two note intervals of this triad, and can now lookup the name of the triad chord quality having these intervals.
Looking at the Triad chord table, the name of the triad chord quality having major(M3) and perfect(P5) note intervals is major.
And so the complete triad chord name prefixes the root note, C#, onto this quality, giving us the C# major chord.
Scale chord names using a,b and c notation
The chord symbol III could be followed by the letter a to indicate that it is C# major chord in root position (ie not inverted) - A-sharp minor scale chord IIIa.
Instead, III could be followed by the letter b to indicate that it is C# major chord in 1st inversion - A-sharp minor scale chord IIIb.
Finally, letter c could be used to indicate that it is C# major chord in 2nd inversion - A-sharp minor scale chord IIIc.
Scale chord names using figured bass notation
In place of the b or c symbols above, figured bass symbols could be used to indicate inversions after the chord number symbols III:
So in this key, III6 refers to the C# major chord in 1st inversion, and III64 refers to the C# major chord in 2nd inversion.
The next scale chord
The next step will need to calculate the triad chord whose root / starting note is next scale note.
To do this, the first column we used in this step, C#, will be moved to the final column of the table.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
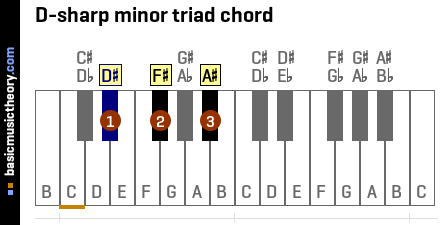
6. 4th triad chord in A-sharp minor scale
Identifying the 3 notes in the chord
The table below shows the A# natural minor scale, ordered to show the 4th note as the first column in the table.
To identify the triad chord note names, use the 1st, 3rd, and 5th columns / scale degrees, which are notes D#, F#, and A#.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | D# | E# | F# | G# | A# | B# | C# |
Identifying the chord quality
To identify the triad chord quality that has these notes, begin by counting the number of half-tones / semitones between the root and each of the notes.
For the 3rd Interval (note 2 on the diagram) the distance between D# and F# is 3 half-tones.
Now look at the complete Note interval table, and identify the note interval that has a distance of 3 half-tones (first column), and with an interval no. of 3 (last column).
The note interval name for the 3rd note / scale degree is therefore minor, also called m3 for short. More details of this interval are at D#-min-3rd.
Repeating this for the 5th note / scale degree, the distance between D# and A# is 7 half-tones, and the note interval name is perfect (P5). More details of this interval are at D#-perf-5th.
Finally, we have the name of the two note intervals of this triad, and can now lookup the name of the triad chord quality having these intervals.
Looking at the Triad chord table, the name of the triad chord quality having minor(m3) and perfect(P5) note intervals is minor.
And so the complete triad chord name prefixes the root note, D#, onto this quality, giving us the D# minor chord.
Scale chord names using a,b and c notation
The chord symbol iv could be followed by the letter a to indicate that it is D# minor chord in root position (ie not inverted) - A-sharp minor scale chord iva.
Instead, iv could be followed by the letter b to indicate that it is D# minor chord in 1st inversion - A-sharp minor scale chord ivb.
Finally, letter c could be used to indicate that it is D# minor chord in 2nd inversion - A-sharp minor scale chord ivc.
Scale chord names using figured bass notation
In place of the b or c symbols above, figured bass symbols could be used to indicate inversions after the chord number symbols iv:
So in this key, iv6 refers to the D# minor chord in 1st inversion, and iv64 refers to the D# minor chord in 2nd inversion.
The next scale chord
The next step will need to calculate the triad chord whose root / starting note is next scale note.
To do this, the first column we used in this step, D#, will be moved to the final column of the table.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
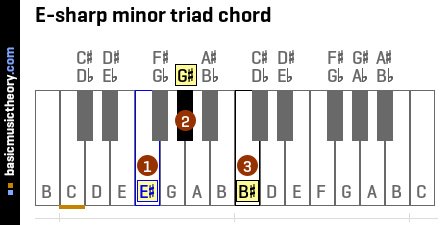
7. 5th triad chord in A-sharp minor scale
Identifying the 3 notes in the chord
The table below shows the A# natural minor scale, ordered to show the 5th note as the first column in the table.
To identify the triad chord note names, use the 1st, 3rd, and 5th columns / scale degrees, which are notes E#, G#, and B#.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | E# | F# | G# | A# | B# | C# | D# |
Identifying the chord quality
To identify the triad chord quality that has these notes, begin by counting the number of half-tones / semitones between the root and each of the notes.
For the 3rd Interval (note 2 on the diagram) the distance between E# and G# is 3 half-tones.
Now look at the complete Note interval table, and identify the note interval that has a distance of 3 half-tones (first column), and with an interval no. of 3 (last column).
The note interval name for the 3rd note / scale degree is therefore minor, also called m3 for short. More details of this interval are at E#-min-3rd.
Repeating this for the 5th note / scale degree, the distance between E# and B# is 7 half-tones, and the note interval name is perfect (P5). More details of this interval are at E#-perf-5th.
Finally, we have the name of the two note intervals of this triad, and can now lookup the name of the triad chord quality having these intervals.
Looking at the Triad chord table, the name of the triad chord quality having minor(m3) and perfect(P5) note intervals is minor.
And so the complete triad chord name prefixes the root note, E#, onto this quality, giving us the E# minor chord.
Scale chord names using a,b and c notation
The chord symbol v could be followed by the letter a to indicate that it is E# minor chord in root position (ie not inverted) - A-sharp minor scale chord va.
Instead, v could be followed by the letter b to indicate that it is E# minor chord in 1st inversion - A-sharp minor scale chord vb.
Finally, letter c could be used to indicate that it is E# minor chord in 2nd inversion - A-sharp minor scale chord vc.
Scale chord names using figured bass notation
In place of the b or c symbols above, figured bass symbols could be used to indicate inversions after the chord number symbols v:
So in this key, v6 refers to the E# minor chord in 1st inversion, and v64 refers to the E# minor chord in 2nd inversion.
The next scale chord
The next step will need to calculate the triad chord whose root / starting note is next scale note.
To do this, the first column we used in this step, E#, will be moved to the final column of the table.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
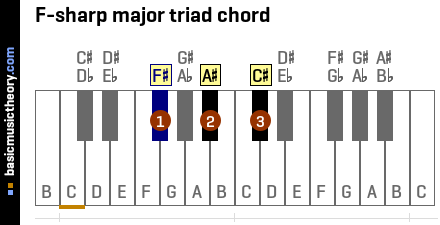
8. 6th triad chord in A-sharp minor scale
Identifying the 3 notes in the chord
The table below shows the A# natural minor scale, ordered to show the 6th note as the first column in the table.
To identify the triad chord note names, use the 1st, 3rd, and 5th columns / scale degrees, which are notes F#, A#, and C#.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | F# | G# | A# | B# | C# | D# | E# |
Identifying the chord quality
To identify the triad chord quality that has these notes, begin by counting the number of half-tones / semitones between the root and each of the notes.
For the 3rd Interval (note 2 on the diagram) the distance between F# and A# is 4 half-tones.
Now look at the complete Note interval table, and identify the note interval that has a distance of 3 half-tones (first column), and with an interval no. of 3 (last column).
The note interval name for the 3rd note / scale degree is therefore major, also called M3 for short. More details of this interval are at F#-maj-3rd.
Repeating this for the 5th note / scale degree, the distance between F# and C# is 7 half-tones, and the note interval name is perfect (P5). More details of this interval are at F#-perf-5th.
Finally, we have the name of the two note intervals of this triad, and can now lookup the name of the triad chord quality having these intervals.
Looking at the Triad chord table, the name of the triad chord quality having major(M3) and perfect(P5) note intervals is major.
And so the complete triad chord name prefixes the root note, F#, onto this quality, giving us the F# major chord.
Scale chord names using a,b and c notation
The chord symbol VI could be followed by the letter a to indicate that it is F# major chord in root position (ie not inverted) - A-sharp minor scale chord VIa.
Instead, VI could be followed by the letter b to indicate that it is F# major chord in 1st inversion - A-sharp minor scale chord VIb.
Finally, letter c could be used to indicate that it is F# major chord in 2nd inversion - A-sharp minor scale chord VIc.
Scale chord names using figured bass notation
In place of the b or c symbols above, figured bass symbols could be used to indicate inversions after the chord number symbols VI:
So in this key, VI6 refers to the F# major chord in 1st inversion, and VI64 refers to the F# major chord in 2nd inversion.
The next scale chord
The next step will need to calculate the triad chord whose root / starting note is next scale note.
To do this, the first column we used in this step, F#, will be moved to the final column of the table.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
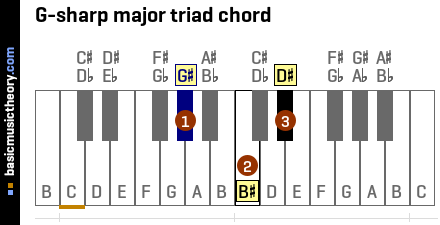
9. 7th triad chord in A-sharp minor scale
Identifying the 3 notes in the chord
The table below shows the A# natural minor scale, ordered to show the 7th note as the first column in the table.
To identify the triad chord note names, use the 1st, 3rd, and 5th columns / scale degrees, which are notes G#, B#, and D#.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Note | G# | A# | B# | C# | D# | E# | F# |
Identifying the chord quality
To identify the triad chord quality that has these notes, begin by counting the number of half-tones / semitones between the root and each of the notes.
For the 3rd Interval (note 2 on the diagram) the distance between G# and B# is 4 half-tones.
Now look at the complete Note interval table, and identify the note interval that has a distance of 3 half-tones (first column), and with an interval no. of 3 (last column).
The note interval name for the 3rd note / scale degree is therefore major, also called M3 for short. More details of this interval are at G#-maj-3rd.
Repeating this for the 5th note / scale degree, the distance between G# and D# is 7 half-tones, and the note interval name is perfect (P5). More details of this interval are at G#-perf-5th.
Finally, we have the name of the two note intervals of this triad, and can now lookup the name of the triad chord quality having these intervals.
Looking at the Triad chord table, the name of the triad chord quality having major(M3) and perfect(P5) note intervals is major.
And so the complete triad chord name prefixes the root note, G#, onto this quality, giving us the G# major chord.
Scale chord names using a,b and c notation
The chord symbol VII could be followed by the letter a to indicate that it is G# major chord in root position (ie not inverted) - A-sharp minor scale chord VIIa.
Instead, VII could be followed by the letter b to indicate that it is G# major chord in 1st inversion - A-sharp minor scale chord VIIb.
Finally, letter c could be used to indicate that it is G# major chord in 2nd inversion - A-sharp minor scale chord VIIc.
Scale chord names using figured bass notation
In place of the b or c symbols above, figured bass symbols could be used to indicate inversions after the chord number symbols VII:
So in this key, VII6 refers to the G# major chord in 1st inversion, and VII64 refers to the G# major chord in 2nd inversion.
This completes the set of all triad chords that harmonize with the A# natural minor scale.
 Bass Clef
Bass Clef
 Treble Clef
Treble Clef
Related Keys and Topics
| Key | C | C# | Db | D | D# | Eb | E | E# | Fb | F | F# | Gb | G | G# | Ab | A | [A#] | Bb | B | B# | Cb |
|---|